Modèle à une couche

In a first approximation, the earth is taken as one spherical layer receiving, reflecting, absorbing and emitting electromagnetic radiations within a star-planet configuration.

Without an atmosphere, a part of the incoming sunlight will be reflected (albedo) and the rest will warm the ground. To maintain a steady state, the total amount of energy received by the planet must be re-emitted to the outer space. The ground will warm up until its surface temperature will reach the level at which its radiation – in the long wave IR range – is in balance with the absorbed flux.

This is the situation of the moon, with an average albedo of 0.12.

Star – Planet configuration

With an atmosphere however, the air will also be warmed up because it absorbs parts of the incoming and of the outgoing radiation. To make a slightly more complex model, a second layer is drawn that represents the “Top of Atmosphere” (TOA) the altitude at which the so-called “characteristic emission level τ” is in equilibrium (see Lapse rate).

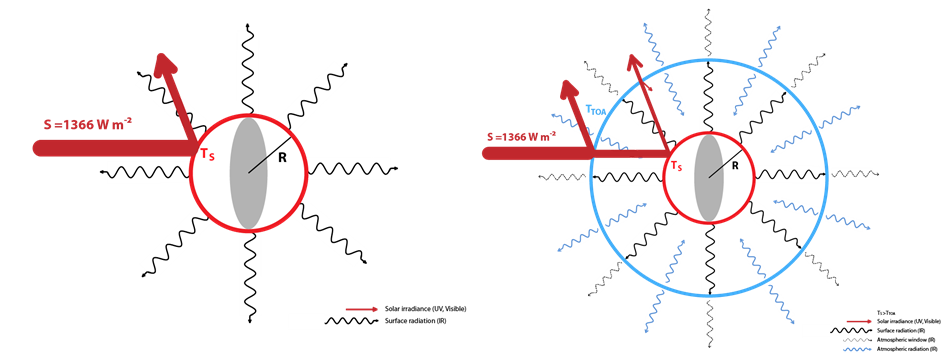
Simple models with one or two layers
In red, solar irradiance (UV, visible, near IR) and reflection
In grey, surface radiation (IR)
In light grey: atmospheric window, the part of surface radiation not absorbed by the atmosphere
In blue: atmospheric radiation (air, clouds, particles)

For both models to satisfy an overall energy balance, all incoming energy must be reflected, or radiated away as long wave radiation. Otherwise, we would never stop frying or freezing.

With such models it is possible to estimate the surface and the TAO temperature, using the Stefan-Boltzmann equation.

One layer model:

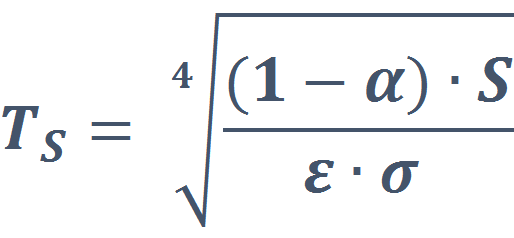eq-ts-1 (eq. 7)

Where:

S is the solar input hitting the surface [W m^-2]
α is the albedo (the portion of incoming light that is readily reflected to the outer space), for the earth 0.306 on average
ε is the black body emissivity

In this model, the role of an atmosphere cannot be calculated. The results for various situations are:

Situation	Parameters	Energy flux W m-2	T Surface °C
Black body at Earth orbit	α = 0 ε = 1	1366	120.8
Black body sphere rotating in 24 h	α = 0 ε = 1	341.5	5.4
Moon at noon vertical	α = 0.12 ε = 0.95	1202	113.4
Moon average	α = 0.12 ε = 0.95	300.5	0.2
Earth Zenith, 12 noon	Max. for solar panels	1000	99.0
Earth average	α = 0.306 ε = 0.92	237.0	-13.5

One layer model calculations

The calculated earth average of -13.5 °C does not correspond to any realistic situation since, without atmosphere and vegetation, and with oceans totally evaporated, the albedo would be similar to the one on the moon. In fact, with an atmosphere, the earth surface temperature is on average 14°C. The alleged “warming thanks to atmosphere and water” would look like bringing air and water to the moon: 13.8 °C and not 27.5 °C.