Correlations deal with facts, and facts are stubborn.
Models deal with human mind, and minds can be ill.
Modelling is already at work when temperature anomalies are averaged over their daily, monthly and yearly changes, and between measuring stations at different locations. To prepare data series like HADRUT4 as represented in the Temperature section, mathematical functions are applied under the assumption that a continuity exists over time and between locations. This may be the cause of heated discussions (which is to be expected when speaking of warming), because human biases may be at play. In the data preparation, this kind of modelling is called massaging because it often consists in smoothing the values. As long as such processing is clearly disclosed there is nothing wrong with it.
Simple models reflect simple phenomena, as for example the application of single known physical laws.
In more complex models various relationships between a large number of variables are assembled together to calculate a desired outcome, such as the flying behaviour of an airplane, the dimensions of a petrochemical plant, or the construction of a gas turbine. Some of the underlying phenomena are calculated by using well known physical equations; in other cases empirical formula derived from regression analysis must be used, in particular for complex systems such as fluid dynamics and heat exchanges. Having such a model at hand, the engineer puts together scenarios consisting in sets of parameters that represent the cases to be analysed. No time-dependant parameters are used in static models, while in dynamic ones, projections of time-dependant parameters are required.
As Molière’s Bourgeois gentilhomme is delighted and surprised to learn that he has been speaking prose all his life, we all are using models without being aware of it.
|
In a first approximation, the Earth is taken as one spherical layer receiving, reflecting, absorbing and emitting electromagnetic radiations within a star-planet configuration. Without an atmosphere, a part of the incoming sunlight will be reflected (albedo) and the rest will warm the ground. To maintain a steady state, the total amount of energy received by the planet must be re-emitted to the outer space. The ground will warm up until its surface temperature will reach the level at which its radiation – in the long wave IR range – is in balance with the absorbed flux. This is the situation of the moon, with an average albedo of 0.12. |
|
|
With an atmosphere however, the air will also be warmed up because it absorbs parts of the incoming and of the outgoing radiation. To make a slightly more complex model, a second layer is drawn that represents the “Top of Atmosphere” (TOA) the altitude at which the so-called “characteristic emission level τ” is in equilibrium (see Lapse rate).
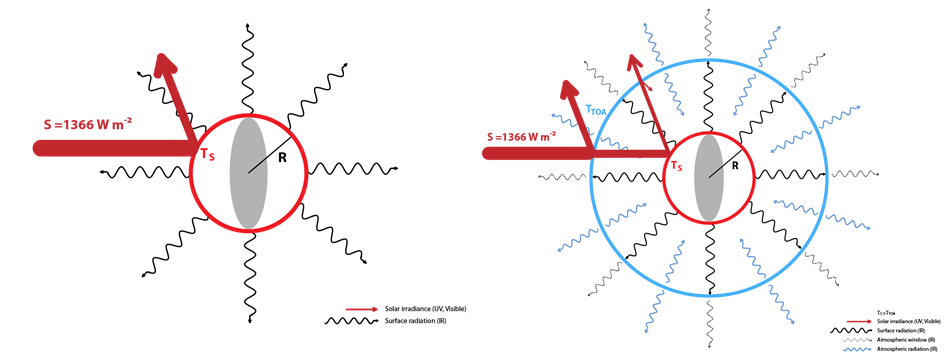
Simple models with one or two layers
In red, solar irradiance (UV, visible, near IR) and reflection
In grey, surface radiation (IR)
In light grey: atmospheric window, the part of surface radiation not absorbed by the atmosphere
In blue: atmospheric radiation (air, clouds, particles)
For both models to satisfy an overall energy balance, all incoming energy must be reflected, or radiated away as long wave radiation. Otherwise, we would never stop frying or freezing.
With such models it is possible to estimate the surface and the TAO temperature, using the Stefan-Boltzmann equation.
One layer model:
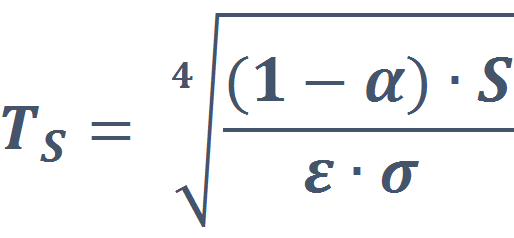(eq. 7)
Where:
- S is the solar input hitting the surface [W m-2]
- α is the albedo (the portion of incoming light that is readily reflected to the outer space), for the Earth 0.306 on average
- ε is the black body emissivity
In this model, the role of an atmosphere cannot be calculated. The results for various situations are:
| Situation | Parameters | Energy flux W m-2 | T Surface °C |
|---|---|---|---|
| Black body at Earth orbit | α = 0 ε = 1 | 1366 | 120.8 |
| Black body sphere rotating in 24 h | α = 0 ε = 1 | 341.5 | 5.4 |
| Moon at noon vertical | α = 0.12 ε = 0.95 | 1202 | 113.4 |
| Moon average | α = 0.12 ε = 0.95 | 300.5 | 0.2 |
| Earth Zenith, 12 noon | Max. for solar panels | 1000 | 99.0 |
| Earth average | α = 0.306 ε = 0.92 | 237.0 | -13.5 |
One layer model calculations
The calculated Earth average of -13.5 °C does not correspond to any realistic situation since, without atmosphere and vegetation, and with oceans totally evaporated, the albedo would be similar to the one on the moon. In fact, with an atmosphere, the Earth surface temperature is on average 14°C. The alleged “warming thanks to atmosphere and water” would look like bringing air and water to the moon: 13.8 °C (from -13.5 to +0.2) and not 27.5 °C (from -13.5 to 14).