When a perturbation is applied to an active and complex system, its primary response will be accompanied by some feedback mechanisms.
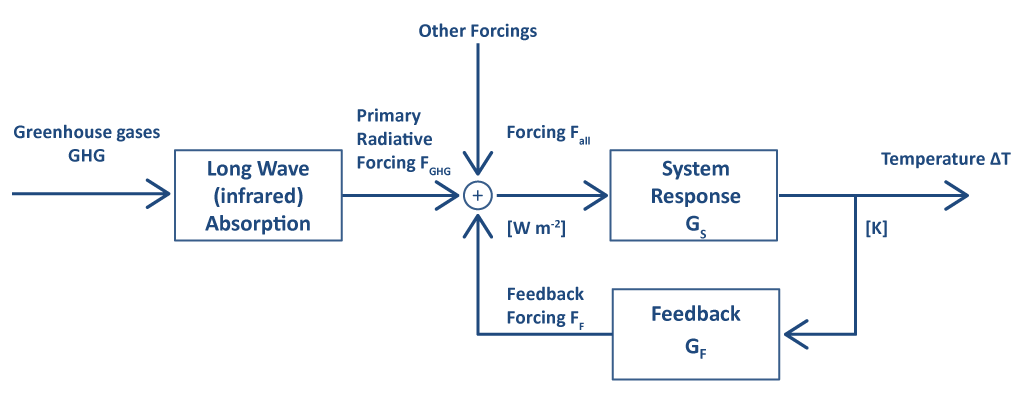
Block diagram of system with feedback
In this diagram the variables are:
- FGHG = Forcing resulting from the absorption of long wave radiations by greenhouse gases
- FF = Forcing resulting from feedback mechanisms [W m-2]
- Fall = FGHG + FF
- ∆T= Surface temperature variation resulting from the total forcing [K]
- GS = Primary system response = ∆T/Fall [K W-1 m2]
- GF = System feedback response = FF/∆T [W m-2 K-1]
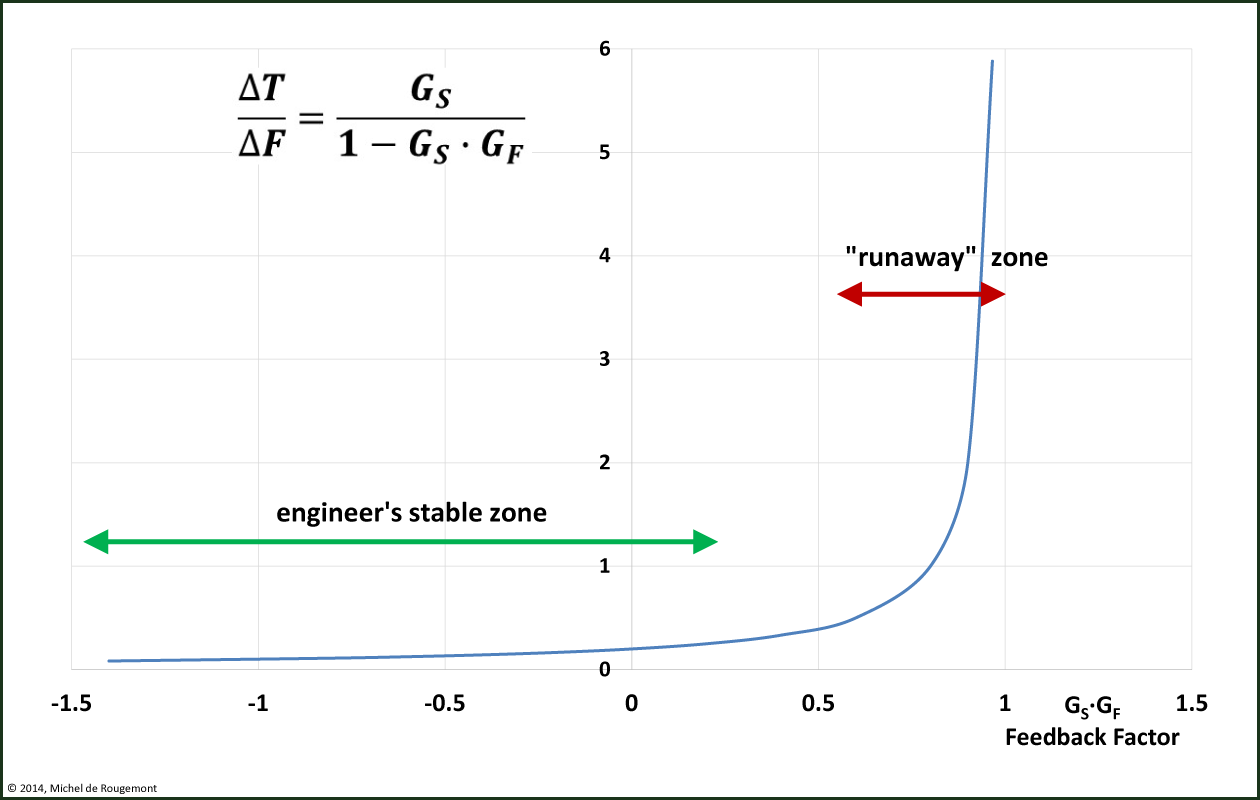
Applying the transfer functions and resolving for ∆T:
∆T = GS· Fall
FF = GF· T
Fall = FGHG + FF =FGHG + GF· ∆T
∆T/GS = FGHG + GF·∆T
∆T·(1- GF·GS)= GS· FGHG
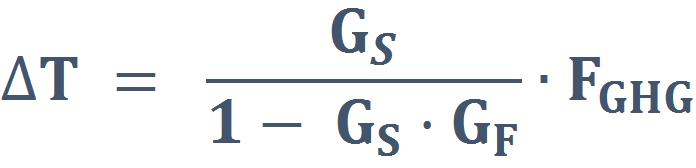 (eq. 12)
(eq. 12)
|
Note that the system goes into total instability with values approaching +1. |
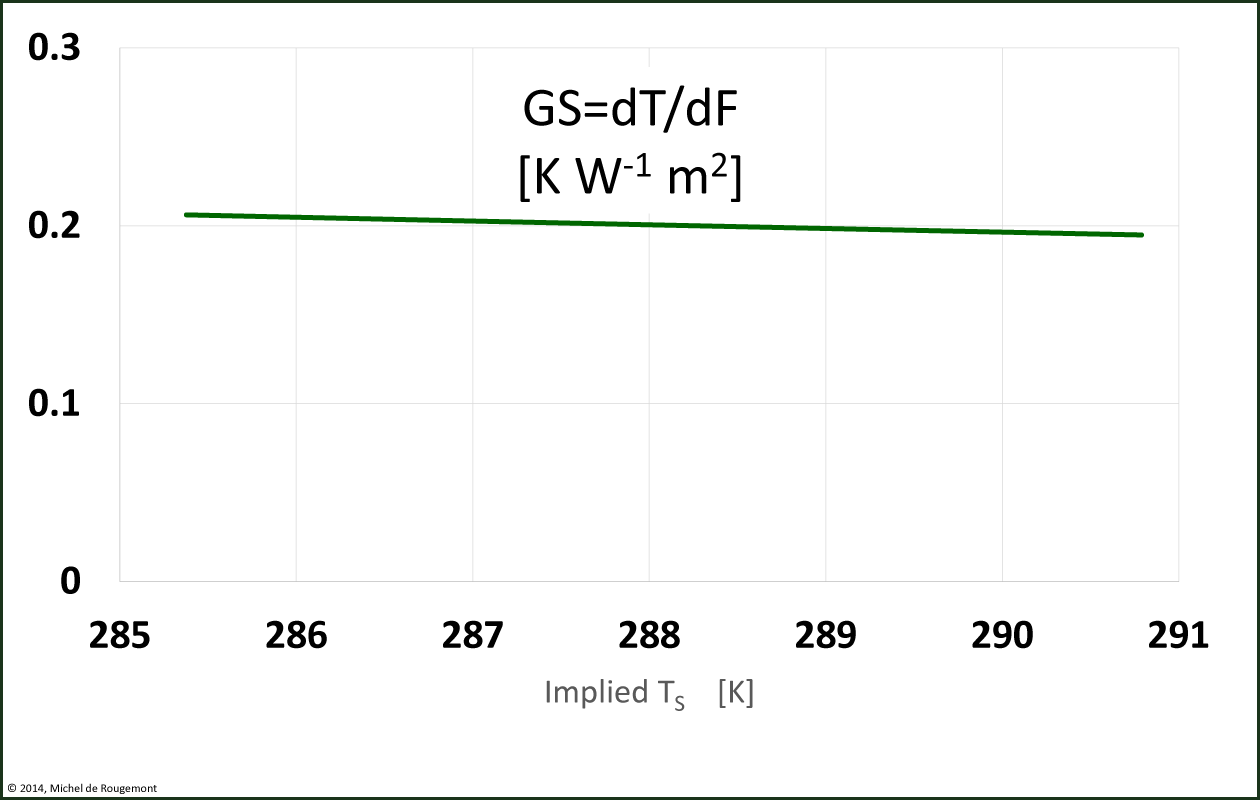
According to the Stefan-Boltzmann equation, the radiation is related to the surface temperature of a grey body:
F = ε·σ·T4 or T = (F/(ε·σ))0.25 thus
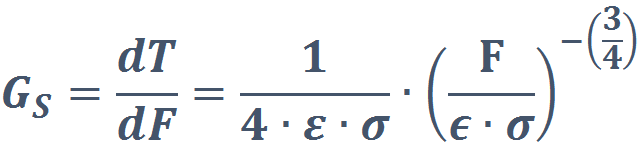 (eq. 13)
(eq. 13)
Where F is a forcing imposed on the top of the underlying system radiation.
|
To simplify, around 287-290 K, the average Earth surface temperature, this transfer function can be linearized at:
GS = 0.200 K W-1 m2 |
|
Feedback transfer function
The feedback transfer function GF is a combination of all mechanisms that will react to the temperature increase caused by the primary forcing exerted by GHGs.
Five feedback mechanisms are considered: Planck, water vapour, lapse rate, albedo, and clouds.
The feedback factor λ associated with each mechanism is defined as the forcing that would result from a temperature change of one degree [W m-2 K-1].
Thirty published values of these feedback factors are presented in the latest IPCC report (AR5 WG1 Chapter 9). Uncertainty is given with 2x the standard deviation, a 90% confidence.
Planck
As temperature increases, the radiative energy emitted will also increase according to Planck law. Part of the temperature increase contributes therefore to eliminate the forcing… and to dampen the temperature rise. Thus, Planck response is a negative feedback:
λP = -3.21 ± 0.11 W m-2 K-1
Water Vapour
More water will evaporate when temperature is increasing. The higher air humidity will absorb more radiative energy and contribute to amplifying the forcing. This is a positive feedback:
λWV = 1.63 ± 0.33 W m-2 K-1
However, the evaporation-condensation of water, with its large latent heat, is not included in this parameter. Another model would be required to reflect this.
Lapse Rate
The lapse rate is described in chapter 2.3.3. When the overall temperature increases the structure of the atmosphere will change, convective force will move warmer air upwards and the gradient will change: this gradient will tend to be less pronounced in tropical latitudes (negative feedback) and more pronounced in mid-latitudes (positive feedback). Overall it results to be a negative feedback, with a large uncertainty:
λLR = -0.60 ± 0.46 W m-2 K-1
Albedo
The reflectivity of the sunlight depends on the type and on the extent of the surface that is reflecting it. In particular there is a large difference between ice and water. With higher temperature less ice or snow coverage is expected, resulting in less reflection. This is a positive feedback:
λA = 0.31 ± 0.11 W m-2 K-1
Clouds
Clouds show two different feedbacks. With higher temperature, water will evaporate and more clouds will be formed. With a larger reflective surface, cloud albedo will increase, more sunlight will be reflected back to the outer space, a negative feedback. But at higher altitude the clouds will contribute to more radiative forcing in the IR range. Overall the current estimate is that it is a positive feedback, albeit with a high uncertainty (300%):
λC = 0.28 ± 0.84 W m-2 K-1
Overall these factors are additive, resulting in a negative feedback:
λ = λP + λWV + λLR + λA + λC = -3.21 + 1.63 – 0.60 + 0.31 + 0.28
and by adding the error ranges:
GF = λ = -1.59 [±1.85] W m-2 K-1
This negative feedback indicates a stabilization of the system in response to the primary forcing. A positive feedback would mean an amplification of the primary effect, up to instability if the feedback factor would approach 1.
Note: the feedback factors are estimates from various models that are summarized by the IPCC in its 5th report. When remembering the sensitivity to basic parameters (albedo, emissivity, and cloudiness) one can only expect that these estimates may change. Also, it looks somehow absurd to evaluate a model with other models’ results, but this is all what we have at this time.
Model with feedback
The energy balance with two layers and the overall feedback can be put together to resolve Eq. 12:
|
With GS set at |
FGHG |
Feedback GF |
ΔTS overall |
|
|
[W m-2] |
Scenario |
[W m-2] |
[K or °C] |
|
|
Since begin of industrial era |
2.59 |
no feedback |
0 |
0.52* |
|
weak feedback |
+0.26 |
0.55 |
||
|
λ |
-1.59 |
0.39 |
||
|
strong feedback |
-3.44 |
0.31 |
||
|
Since begin of industrial era |
1.91 |
no feedback |
0 |
0.38 |
|
weak feedback |
+0.26 |
0.40 |
||
|
λ |
-1.59 |
0.29 |
||
|
strong feedback |
-3.44 |
0.23 |
||
|
With any doubling of CO2 |
3.71 |
No feedback |
0 |
0.74 |
|
weak feedback |
+0.26 |
0.78 |
||
|
λ |
-1.59 |
0.56 |
||
|
strong feedback |
-3.44 |
0.44 |
||
Climate sensitivity to radiative forcing, before and after feedback.
* the slight difference from the previous table is due to the linearization of GS.
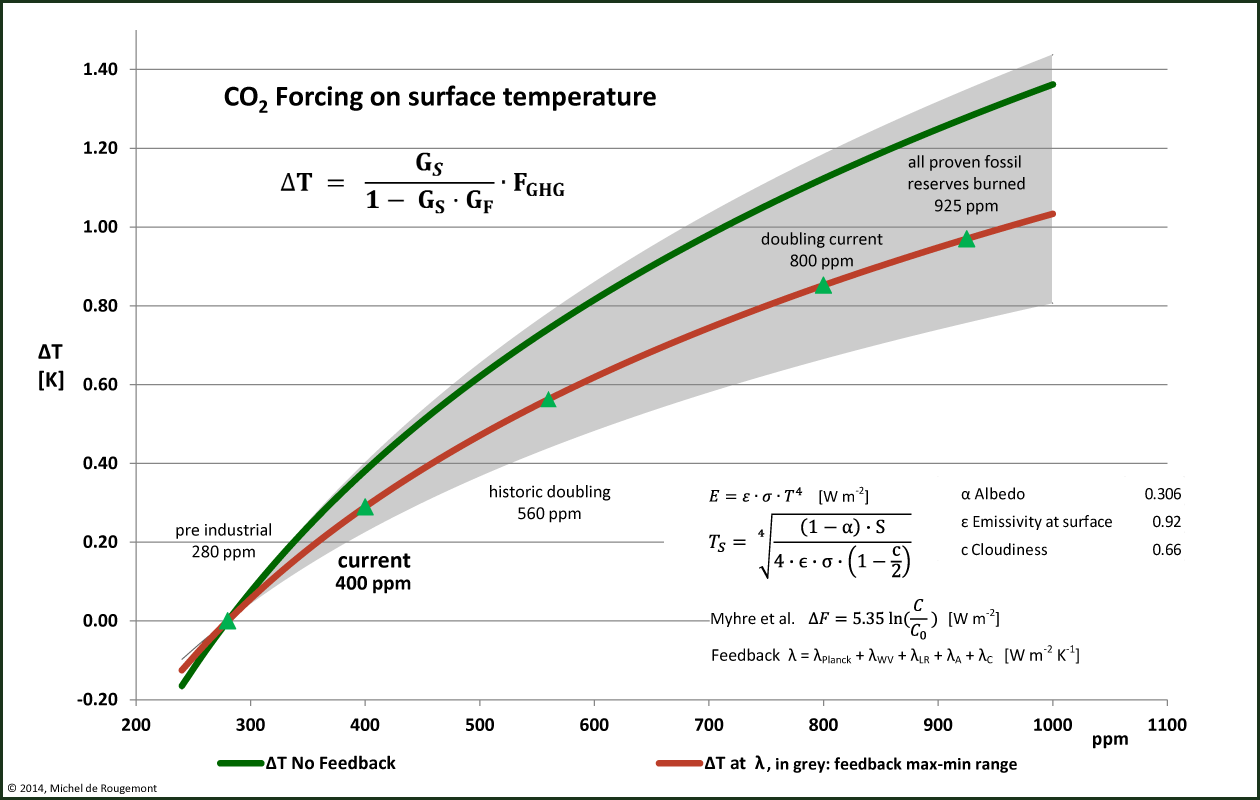
The same calculations can be made for tentative CO2 concentrations at pre-industrial time, or in a possible future. In following diagram error margins mentioned above for the feedback factors are also represented.
This is incredibly not new, but astonishing!
Temperature response to radiative forcing by CO2 alone with feedback.
Read like this:
with currently 400 ppm, CO2 contribution to warming is 0.29 °C when including a feedback of -1.59 W m-2 K-1.
Or: when the historic CO2 concentration will have doubled to reach 560 ppm, the temperature will have increased by an additional 0.27 °C (total “equilibrium temperature sensitivity” = 0.56 °C).
Or: if the feedback is weak (even slightly positive), the current CO2 contribution to warming may be 0.40 °C