Surface temperature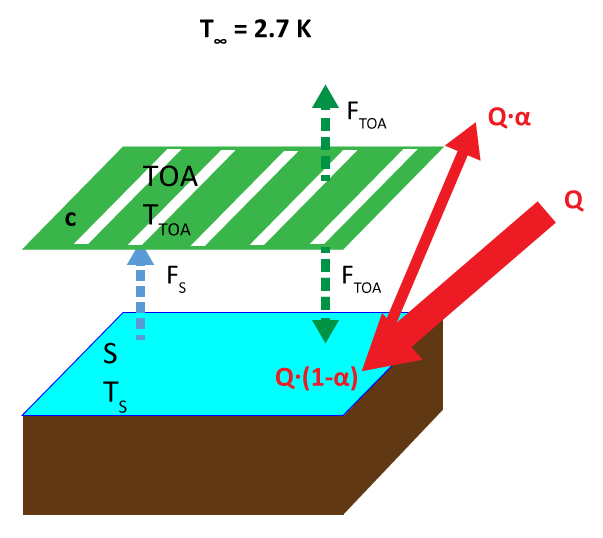
The incoming solar radiation oat the earth's orbitaé distance is S=1366 Wm-2. On avergare, to account for the spericity of the planet and its 24 h rootation, the averagge incident irradiation Q ist one fourth of the solar constant Q = S/4.
For the two surfaces and the fluxes shown on the model picture, the energy balance is[1]:
Energy absorbed + Energy received from 2nd layer = Energy emitted at surface
![]() (eq. 8)
(eq. 8)
At the Top of Atmosphere
Energy received from the surface = 2 x energy emitted from TOA[2]
![]() (eq. 9)
(eq. 9)
Where:
- FS and FTOA are the energy fluxes at the Surface and at the Top of Atmosphere,
- S is the solar constant, the radiation as received on the Earth orbit (1366 W m-2),
- c is the cloudiness ratio, the portion of the sky covered by clouds,on average 66%,
- R is the Earth’s radius. It is taken as the same for the top of atmosphere as for the surface, an acceptable approximation (6-10 km in relation with 6357 km).
Radiative Forcing ΔF can be added to these energy fluxes.
Applying the Stefan Boltzmann equation gives:
![]() and
and ![]()
Solving equations 8 and 9 for FS and FTOA gives:
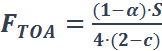 and
and 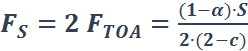 , thus
, thus
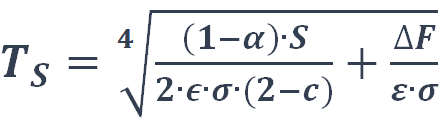 (eq. 10), and
(eq. 10), and 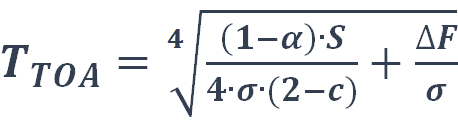 (eq. 11)
(eq. 11)
To calculate TS and TTOA , parameters must be selected within a realistic range.
With α = 0.306, ε = 0.92 at the Earth’s surface, and c = 0.66 the results are:
|
Emitted radiation |
Temperature |
||
|
K |
°C |
||
|
At the Earth’s surface, TS |
353.7 |
287.0 |
+13.8 |
|
At the top of atmosphere TTOA |
176.9 |
236.3 |
-36.8 |
Surface and Top of Atmosphere temperature
by application of eq. 10 and 11 with actual conditions
These calculated figures are quite well in line with observed values. A temperature of -37°C correspond to an altitude of 5700 m (ISA standard). The simple two layers model is therefore validated as plausible.
Parameter Sensitivity
In this model, the surface temperature is defined by just 4 parameters. Variations of solar input are known and of cyclical nature: orbital ellipse, solar spots, Milankovitch cycles. The sensitivity of TS to these parameters can be evaluated:
- For each 1 W m-2 increase of solar constant S, TS and TTOA will increase by 0.05 °C
- For each 0.01 increase of albedo α, TS decreases by 1.04 °C, and TTOA by 1.15 °C.
- For each 0.01 increase of cloudiness c, TS increases by 0.54 °C, TTOA by 0.45 °C.
- For each 0.01 increase of surface emissivity ε, TS decreases by 0.78 °C.
- For each 1 W m-2 due to radiative forcing, TS will increase by 0.20 °C, and TTOA by 0.33 °C.
Notes:
- Variations of solar input are known and of cyclical nature: orbital ellipse, solar spots, Milankovitch cycles.
- Even with the most sophisticated remote sensing technologies, the measurement of α, c, and ε are quite inaccurate because of the large differences across the latitudes, of surface properties (land, vegetation, water, snow, ice), and between seasons. In addition, they are not independent from each other since albedo will change with cloudiness. These issues will not disappear with more sophisticated models. See also feedback mechanisms below.
- Temporary disequilibrium of the energy balance takes place each day and over the seasons. Other heat accumulation and release phenomena happen in the oceans (e.g. El Niño), eventually with long time lags (annual, decadal, or more).
- Heat fluxes from the core of the Earth (geothermal flux, approx. 0.082 W m‑2), from the release of fossil and nuclear energy by human activities (approx. 0.03 W m-2), or from change in biomass are very minor components of the energy balance and are not highly variable. They can be ignored in this model calculation.
[1] For model explanations see Stocker, T., Lecture notes, “Einführung in die Klima Modellierung.“ http://www.climate.unibe.ch/~stocker/papers/stocker08EKM.pdf
[2] It takes some explanation to understand that energy is bouncing back and forth between the surface and the emitting layer at TOA without being actually exchanged.
A thought experiment: when, in a long floor well isolated toward the exterior, two facing walls are at the same temperature, they emit the same amount of energy toward each other. On balance, they re-emit what they receive. If the temperature of one of the walls increases (e.g. by heating it from the exterior) the other one will warm until a new equilibrium is reached. The first thermodynamic principles is respected.


