Heat is a form of energy contained in more or less warm material. When two bodies that have a different temperature are put in contact, heat will be exchanged until the temperature difference will have vanished. There are three heat exchange mechanisms.
Conduction
Heat is propagated by the transmission at microscopic scale of the thermal agitation of the material.
 (eq. 1) (eq. 1) |
 |
where:
- q is the heat flux [W],
- k is the thermal conductivity of the material [W m-1 K-1 ],
- A is the area where the heat transfer takes place [m2],
- ΔT is the temperature gradient (difference) across the material [K],
- s is the thickness of the material [m].
Depending on their atomic or molecular structure, materials have different thermal conductivity:
| Material | Thermal conductivity [W m-1 K-1 ] |
|---|---|
| Diamond | 1000-2600 (if your hand is full of diamond this feels very cool!) |
| Silver | 418 |
| Copper | 390 |
| Aluminium | 237 |
| Marble | 2.1 - 3 |
| Glass | 1.2 |
| Concrete | 0.92 |
| Soil | 0.2 – 4 (depending of humidity) |
| Wood | ~ 0.15 (more conductive if wet) |
| Polyurethane foam | 0.025 |
| Water (liquid) | 0.6 |
| Ice (at 0 °C) | 0.22 |
| Air (std. pressure) | 0.0262 |
- Thermal conductivities at 20 °C
Source: Wikipedia and www.engineeringtoolbox.com
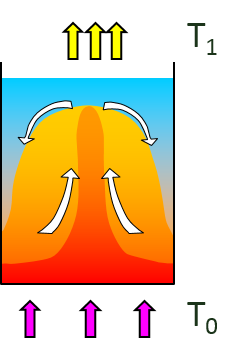
Convection
| Heat is transferred by the movement of a fluid from one place to another. The
equation describing the convective heat transfer is the same as for conductive, but with a major difference: the heat transfer coefficient and the thickness of the layer where the exchange takes place are highly dependent of conditions of flow and of the temperature of the moving fluid. Example: the warm ground transfers its heat to air (as long as this air is colder than the ground), the lighter warmed air rises and warms the atmosphere at higher altitude. Heat transfer can be enhanced by forced convection: by winds or mechanical agitation. Convective heat transfer is already a very complex process, difficult to determine by exact equations taking into account all influencing parameters. This is why empirical formulas are used for engineering purposes, of course within acceptable ranges of application. As for example the convective heat transfer around an object moving in air at velocity v can be approximated by: hc = 10.45 - v + 10 v1/2 [W m-2 K-1] |
 |


