Matter absorbs electromagnetic radiations and, as long as equilibrium is not reached, is heated by the quantity of energy that it absorbs. In the whole discussion about climate and the heat balance around the Earth, the relevant frequencies of these radiations are in the range from high energy ultraviolet (UV) down to long wave infrared.
Solids may not absorb light but reflect it, as mirrors do. A perfect mirror would reflect all incident light without any loss of energy, like a Ping-Pong ball rebounds on the table. But in reality only a fraction of the incident radiation will be reflected; the reflective behaviour of a surface is called albedo α, having a value of 1 when reflecting all light and 0 for total absorption.
| Surface | Albedo |
|---|---|
| Fresh asphalt | 0.04 |
| Worn asphalt | 0.12 |
| Conifer forest (Summer) | 0.08 to 0.15 |
| Deciduous trees | 0.15 to 0.18 |
| Bare soil | 0.17 |
| Green grass | 0.25 |
| Desert sand | 0.40 |
| New concrete | 0.55 |
| Open ocean | 0.06 (depending on zenith angle) |
| Ocean ice | 0.5–0.7 |
| Fresh snow | 0.80–0.90 |
| Earth average | 0.306 (NASA Earth fact sheet) |
| Moon average | 0.12 (NASA Moon fact sheet) |
Typical albedos
Source: Wikipedia, if not noted otherwise.
Material with a low albedo have a high emissivity, and vice versa. However, both factors cannot be interchanged (ε ≠ 1-α).
The part of the electromagnetic radiation that has not been reflected will be absorbed and warms the material until reaching thermal equilibrium by electromagnetic emission of the same energy quantity to the surrounding.
Incoming sunlight
The incoming sunlight has an actual spectra that is different from the one shown on Figure 45. This is due to inhomogeneity of the sun surface and to the partial absorption of the incoming light on its way to the Earth.
Ozone and oxygen are strong absorbers of UV light. At higher wavelength the absorption bands are caused by the gases such as water vapour and carbon dioxide that are present in the atmosphere.
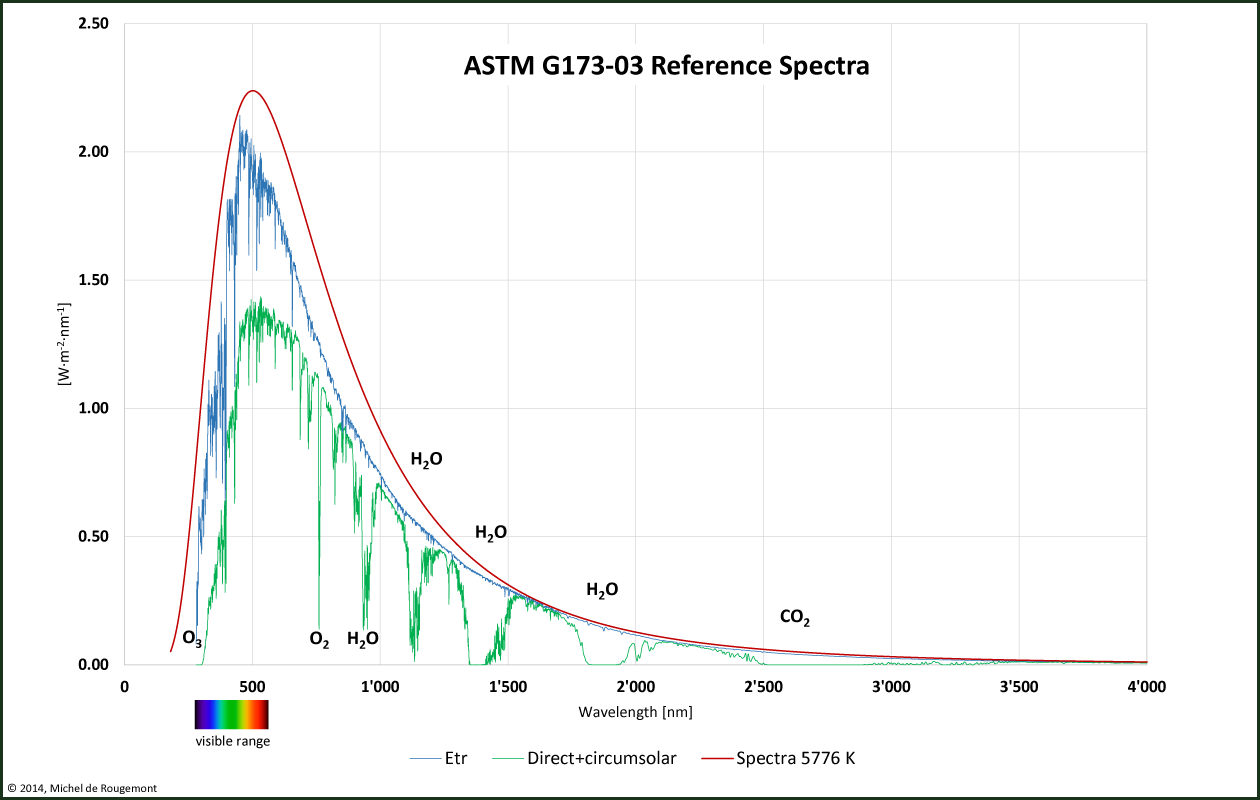
Incoming solar radiation
Etr: extraterrestrial radiation, as measured at the “top of atmosphere” (TOA)
Direct + circumsolar: radiation measured at sea level by clear sky
Spectra 5776 K: calculated for a black body a 5776 K (5503 °C)
Absorption by greenhouse gases
So-called greenhouse gases (GHG) are substances that absorb long wave infrared electromagnetic radiation. Each IR absorbing gas like CO2, H2O, CH4, or N2O has an own absorption spectrum that can be calculated line by line from the possible rotational and vibrational transitions that the given molecule allows; this includes all isotopes of the elements H, C, N, O that form these molecules, in proportion of their abundance.
Radiation spectra can be reconstructed by using the absorption spectra available for download from the HITRAN Database with a 0.1 cm-1 resolution at http://spectra.iao.ru/.
I made this for dry and wet air at the same conditions: T=281.7 K, p= 0.882 atm, over a 2000 m path.
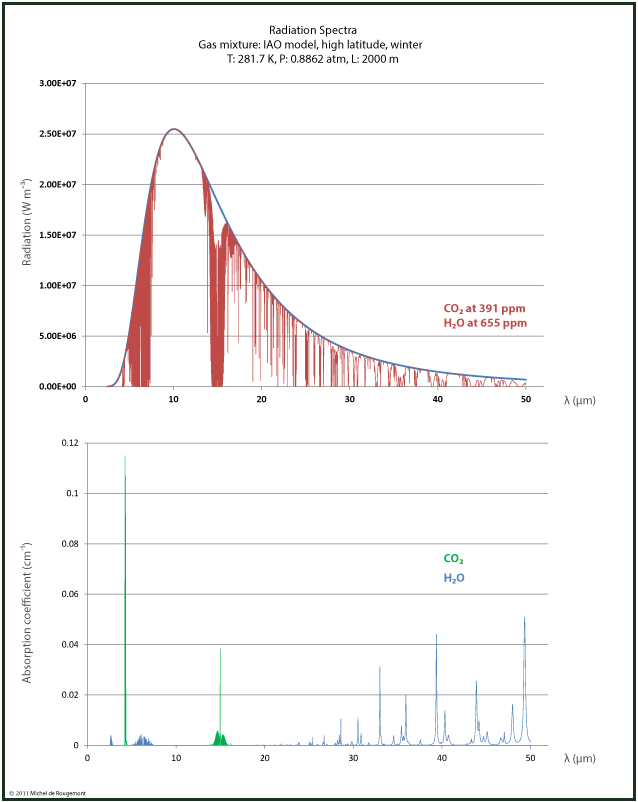 |
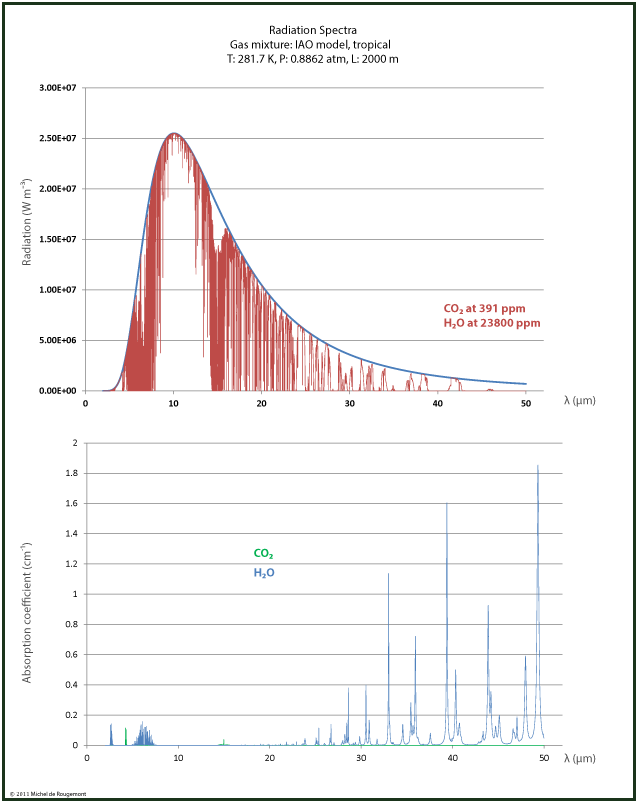 |
| Radiation and absorption spectrum for dry air IAO model with CO2 at 391 ppm, H2O at 655 ppm T=281.7 K, p= 0.882 atm, path 2000 m. |
and for wet tropical air IAO model with H2O at 23800 ppm |
This peak shift implies a more complex absorption pattern when various emitting black bodies are simultaneously at different temperatures, as it is the case in actual atmospheric and land conditions.
Note the much larger water contribution in the wet air due to its higher concentration. But in the 15 μm range, the effect due to CO2 remains the same.
Also in the 15 μm range, the absorption is 100% for some lines but not for all, as can be seen in the zoomed spectrum:
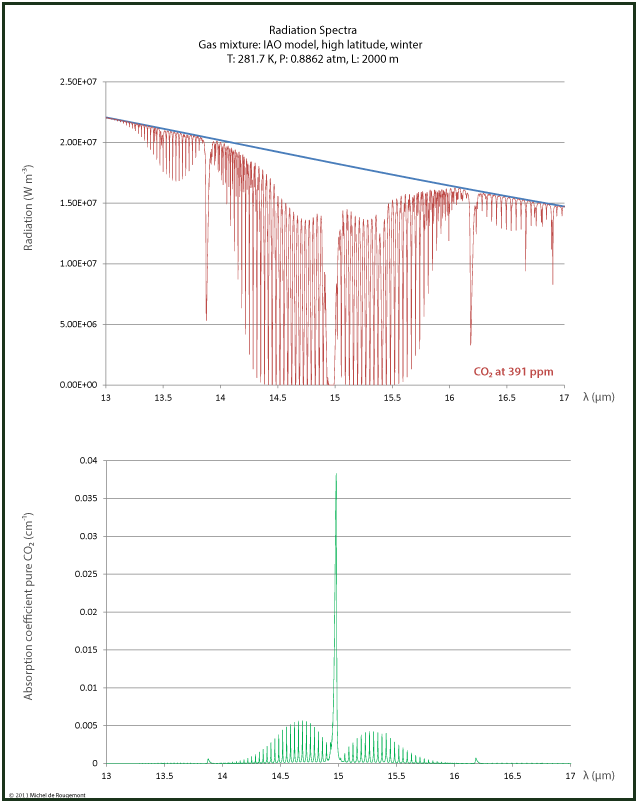
Radiation and absorption spectrum around 15 μm
The black body radiation spectrum is temperature dependant (Wien displacement):
|
Temperature |
Radiation peak |
|
288 K (15°C) |
10.06 μm |
|
287 K (14°C) |
10.10 μm |
|
273 K (0°C) |
10.61 μm |
|
233 K (-40°C) |
12.44 μm |
This peak shift implies a more complex absorption pattern when various emitting black bodies are simultaneously at different temperatures, as it is the case in actual atmospheric and land conditions.
Energy absorbed by IR absorbing gases
The energy absorbed is calculated by the integral of the difference between the undisturbed radiation spectra and the absorption spectra (the surface between the two curves).
The higher the concentration of an absorbing gas the larger the energy amount that will be absorbed. According to the Lambert-Beer law the concentration dependency is logarithmic:
![]() (eq. 5)
(eq. 5)
Where:
- L = path length [m]
- α’ = σ·N, absorption coefficient composed of the absorption cross section σ and the atomic density N (that is proportional to the concentration). [m-1]
Therefore, the energy absorption will depend on the GHG concentration.
Concern has been expressed that this concentration relationship is not true since the atmospheric CO2 would be in such abundance that the absorption would be already saturated and any concentration increase would have no further effect.
The graph on the right shows that the saturation theory cannot be confirmed:
There are clear differences in the radiance calculated at 280 ppm CO2 (the historic level), 391 ppm (the 2011 level), and 600 ppm (an alleged projection for the year 2100).
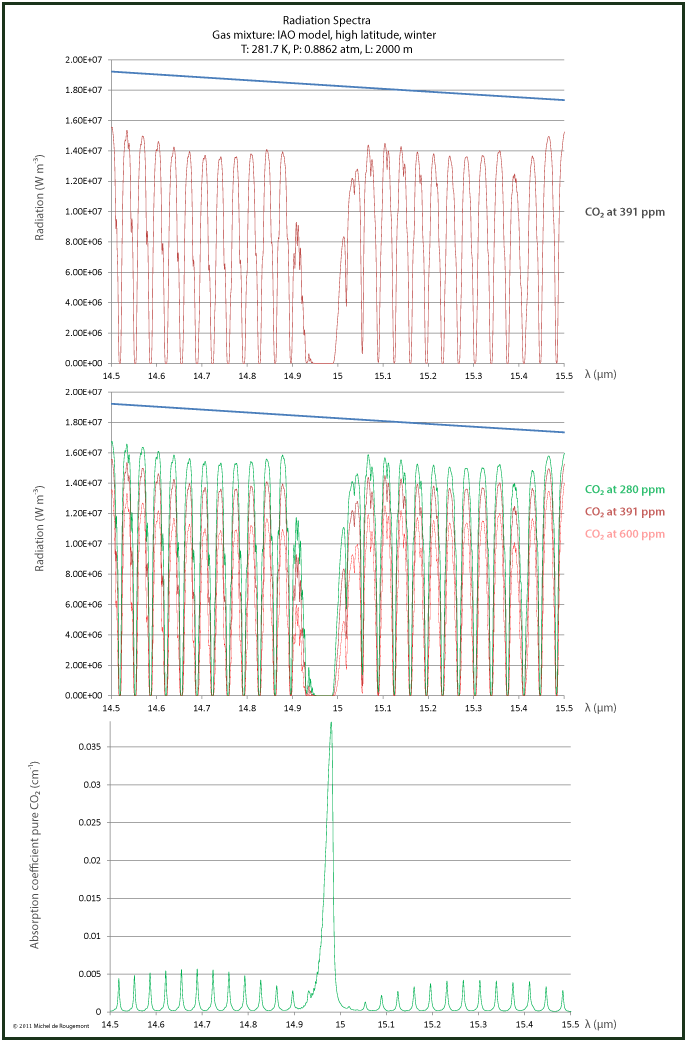
Radiance at three different CO2 concentrations


